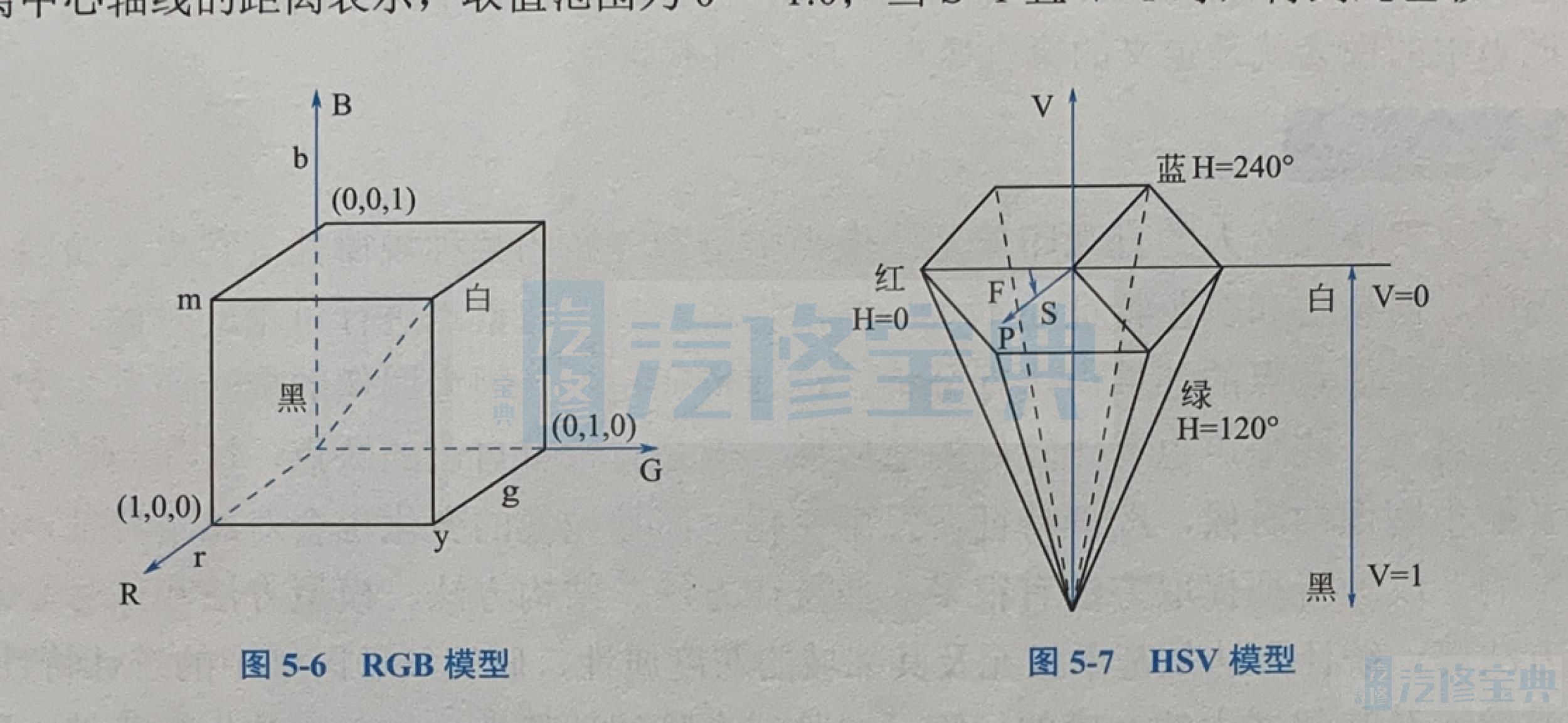
要对图像当中的物体进行分类,就需要先知道图像当中各个部分的特征,利用这些特征作为划分的标准。从某种意义上说,特征的合适与否对分类的精确度起着决定性作用。图像中的特征最基本的是颜色,除此之外,还有纹理、形状等个体的特征以及空间位置关系这种整体的特征。 1.颜色特征颜色特征就是对图像或者图像区域当中色彩的一个描述,它的特点是并不关注细节,不关注具体的某一个像素,而是从整体上来统计图像或者图像区域中的色彩。颜色特征有它自己的优点,比如颜色是不会因为旋转图像发生变化的,即使是放大或者缩小图像,也一样不会有影响。但是这样一来颜色特征也不太适用于对图像中的某一局部进行描述。在图像处理中,常用的颜色特征包括颜色直方图、颜色集、颜色矩、颜色聚合向量等。 (1)颜色直方图颜色直方图是对不同灰度级在图像中所占比例的一个统计分析,它的优点和缺点都在于它的计算与像素点的空间位置无关,它是一个完全的统计特性。这样一方面计算方便,对于不需要考虑空间位置的问题很适用;另方面对于识别出物体的具体位置就显得不适用了。常用RGB、HSV、HSI等颜色空间下的图像来计算图像的颜色直方图。 ①RGB模型也称加色法混色模型,它是将彩色信息分成三个分量(R、G、B分别代表红、绿、蓝),三个分量的不同组合可以表示出不同的颜色。RGB模型可以建立在三维坐标系统中,三个坐标轴分别用RGB的三个分量R、G、B表示,如图5-6所示。RGB模型的空间是一个正方体,原点代表黑色,对角顶点代表白色,RGB颜色空间中的任意一种颜色可以用从原点的矢量表示般情况下,要将RGB颜色模型立方体归一化为单位立方体,此时RGB每个分量的值在[0,1之间。RGB颜色模型的优点是看起来比较直观,缺点是R、G、B三个分量相互依赖,任何一个分量发生改变,都会影响到整体颜色的改变。
RGB模型是人眼最直观的颜色模式,大多数彩色摄像机都是用RGB格式获取图像,能够直观地表示物体的色彩,是一种重要的颜色模型。
②HSⅤ模型用色调(H)、饱和度(S)和亮度(V)三种属性表达颜色特征。
其中色调是与混合光谱中的光的波长相联系的,反映了人们对颜色种类的感受;
饱和度与色调的纯度有关,表示颜色的浓度;亮度表示人眼感受颜色的强弱程度,颜色中掺入白色越多就越明亮。这三种属性能够独立表达人们感受颜色的过程,互相不受影响。因此, HSⅤ模型也称主观颜色模型。
HSⅤ模型也称六角锥体模型,如图5-7所示,色调H用绕中轴旋转的角度表示,取值范围为0~360°,红色为0,按逆时针角度方向计算,绿色为120°,蓝色为240°;亮度V用垂直轴线上的大小表示,取值范围为0~1.0;饱和度S用离中心轴线的距离表示,取值范围为0~1.0;当S=1且V=1时,得到纯色彩。
HSV模型有两个显著特点:第一,在HSV模型中亮度分量V和色度分量H是相互独立的,V分量与图像的颜色无关,只与图像的光照强度有关;第二,色调分量H及饱和度分量S互相独立,并且与人们感知色彩的方式紧密相连。这些优点使得HSV模型可以充分发挥色度分量H的作用,适合基于人类的视觉系统对彩色图像分析的算法。
③HSI色彩模型较好地反映了人们的视觉系统对不同色彩的感知方式,在该模型中用色调(H)、色饱和度(S)及强度(I)三个基本分量来表达不同的颜色。
H与光波的波长紧密相关,不同H的值代表着不同的颜色,如当H值的取值范围为0~360时,红色、绿色和蓝色的H值分别为0、120和240;S代表颜色的纯度,纯色是完全饱和的,颜色也最鲜艳,向纯光谱色中加入白光会降低饱和度;I表示成像的亮度和图像的灰度,I是一个主观的概念,表达了人类视觉对颜色明亮程度的感知。I与图像的彩色信息无关,H和S与人们感受颜色的方式紧密相连,因此,HSI颜色模型得到了广泛的应用,成了颜色检测及分析的常用模型。
(2)颜色集颜色集可以看作是颜色直方图的一个变种,或者说近似。颜色
集的计算需要在视觉均衡的颜色空间中进行,比如HSV颜色空间。所以计算时首先将RGB颜色空间转化到此颜色空间。然后把颜色空间分成若干个柄,再以色彩特征把图像划分成若干子图像。对于三个颜色分量,只保留其中一个量化此颜色空间,并用这个颜色分量作为索引,从而用一个二进制颜色索引集来表达完整的图像。
(3)颜色矩 颜色矩是用来表达图像或者图像区域中颜色分布的一种方法常用的有三种,即颜色的一阶矩(均值)、二阶矩(方差)以及三阶矩(偏斜度)。
它们可以比较充分地来表达一幅图像或者图像区域中的色彩分布。
(4)颜色聚合向量 在求解颜色聚合向量时,首先要获取图像的直方图,然后利用它把其中每个柄的像素划分成两个部分。划分的方法是先给定一个阈值,然后统计柄当中部分像素占据的连续面积,如果它们大于这个阈值,那么这个区域当中的像素就是定义的聚合像素,反之则不是。
2.纹理特征
纹理特征给人的直观印象是图像当中色彩分布的某种规律性,它也是面向全局的。但是它和颜色特征还不太一样,它在对每个像素点进行讨论的时候,往往需要在此像素点的邻域内进行分析。纹理特征是不会因为图像的旋转而发生变化的,对于一些噪声也有比较好的适应性。但是它也有自己的缺点,比如当放大或者缩小图像的时候,纹理特征会发生变化,而且光线的变化也会对纹理特征产生影响。纹理特征提取方法有很多,如统计方法、结构方法、模型方法和信号处理方法等。统计方法是基于像元及其邻域的灰度属性,研究纹理区域中的统计特性,或像元及其邻域内的灰度的一阶、二阶或高阶统计特性,如灰度共生矩阵法;结构方法是基于纹理基元分析纹理特征,着力找出纹理基元,认为纹理由许多纹理基元构成,不同类型的纹理基元、不同的方向和数目等,决定了纹理的表现形式,如数学形态学法;模型方法中,假设纹理是以某种参数控制的分布模型方式形成的,从纹理图像的实现来估计计算模型参数,以参数为特征或采用某种分类策略进行图像分割,如随机场模型法;信号处理方法是建立在时域、频域分析与多尺度分析基础上,对纹理图像中某个区域内实行某种变换后,再提取保持相对平稳的特征值,以此特征值作为特征表示区域内的一致性以及区域间的相异性,如小波变换方法。信号处理方法是从变换域中提取纹理特征,其他方法是从图像域中提取纹理特征。
3.形状特征形状特征的提出主要是为了讨论图像或者图像区域当中物体的各种形式的形状。这里的形状包含了图像或图像区域的周长、面积、凹凸性以及几何形状等特
征。按照形状特征的关注点不同,一般把形状特征分为着眼于边界的特征和关系到整个区域的特征。比较成熟的形状特征描述方法有边界特征法,它着眼于图像中的边界,借以描述图像的形状,采用 Hough变换提取直线和圆就是这类方法的典型应用;傅里叶形状描述符法是针对物体的边界进行傅里叶变换,因为边界有封装和周期性的特征,它可以把二维的问题降成一维;几何参数法是利用形状的定量计算来描述形状特征,计算的参数包括矩、面积、周长、圆度、偏心率等。
4.空间关系特征图像当中的物体是丰富多彩的,物体作为一个独立的个体会有它自己的特性而从整体来看,物体和物体之间也会存在一定的联系,其中最直接的联系就是空间位置关系。比如物体之间可能邻接,也可能是被其他物体间隔的。物体和物体之间可能有相互重叠的情况,也有互不关联的状况。在描述空间位置的时候有时候用绝对的描述,比如用具体的图像中的坐标;也可以用相对的描述,比如相对某一物体的左或者右等。空间位置关系的作用是加强了图像当中物体彼此区分的能力。但是存在的问题是空间位置关系随着图像的旋转会发生变化,而尺度的变化也同样会影响它的效果。正是因为这个特点,一般都要将空间位置关系和其他特征配合起来使用。